Теория вероятностей (семинары Б06-106)

📹
Видео лекции. Райгородский А. М. Осень 2021 [playlist]
📑
Lecture notes (in English - Computer science program) [download]
Вопросы на зачет [download]

Задачи

Семинар 1.  Комбинаторика

Семинар 2.  Классическая вероятность

Семинар 3.  Геометрическая вероятность, схема Бернулли.

Семинар 4.  Условная вероятность.

Семинар 5.  Дискретные cлучайные величины.

Семинар 6.  Непрерывные случайные величины.

Контрольная работа 1

Семинар 7.  Независимость величин, формула свертки.

Семинар 8. Матожидание дискретных случайных величин.

Семинар 10. Матожидание непрерывных случайных величин.

Семинар 11. Характеристическая функция.

Семинар 12. Предельные теоремы. ЦПТ

Посещаемость и оценки

Посещаемость.

Оценки.

Критерии оценок

  • Диф. зачёт. (как экзамен, т.е. будут теоретические вопросы)
  • 2 контрольных работы
  • Посещаемость

Обратите внимание на то, что для успешной сдачи зачета, необходимо получить хотя бы один балл на устном зачете.

Правила проведения устного зачета:

вы получите билет и у вас будет 30 минут на подготовку. Вы сможете пользоваться любыми письменными или печатнами материалами (только свои, нельзя попросить у соседа), но нельзя пользоваться телефоном (интернет) и общаться с вашими соседями. Когда будете готовы сдавать билет, то имеете право пользоваться только тем, что вы написали в течение подготовки в вашей чистой третрадке. (То есть, во время сдачи нельзя пользоваться конспектами или книгами).

Программа курса

  1. Классическое (комбинаторное) определение вероятности. Свойства вероятности при таком определении. Формула включений и исключений (б/д). Задача о беспорядках.
  2. Геометрические вероятности и их свойства. Пример задачи, для решения которой удобно использовать геометрические вероятности (задача о встрече).
  3. Условные вероятности, умножение вероятностей, формулы полной вероятности и Байеса. Независимость событий: попарная независимость, независимость в совокупности, соотношение между видами независимости.
  4. Схема испытаний Бернулли. Понятие о случайном блуждании и случайном графе.
  5. Предельная теорема Пуассона. Интегральная предельная теорема Муавра – Лапласа (б/д; см., впрочем, п. 20). Пример применения теоремы Муавра – Лапласа в задаче о гардеробах.
  6. Общая вероятностная модель. Аксиоматика Колмогорова.
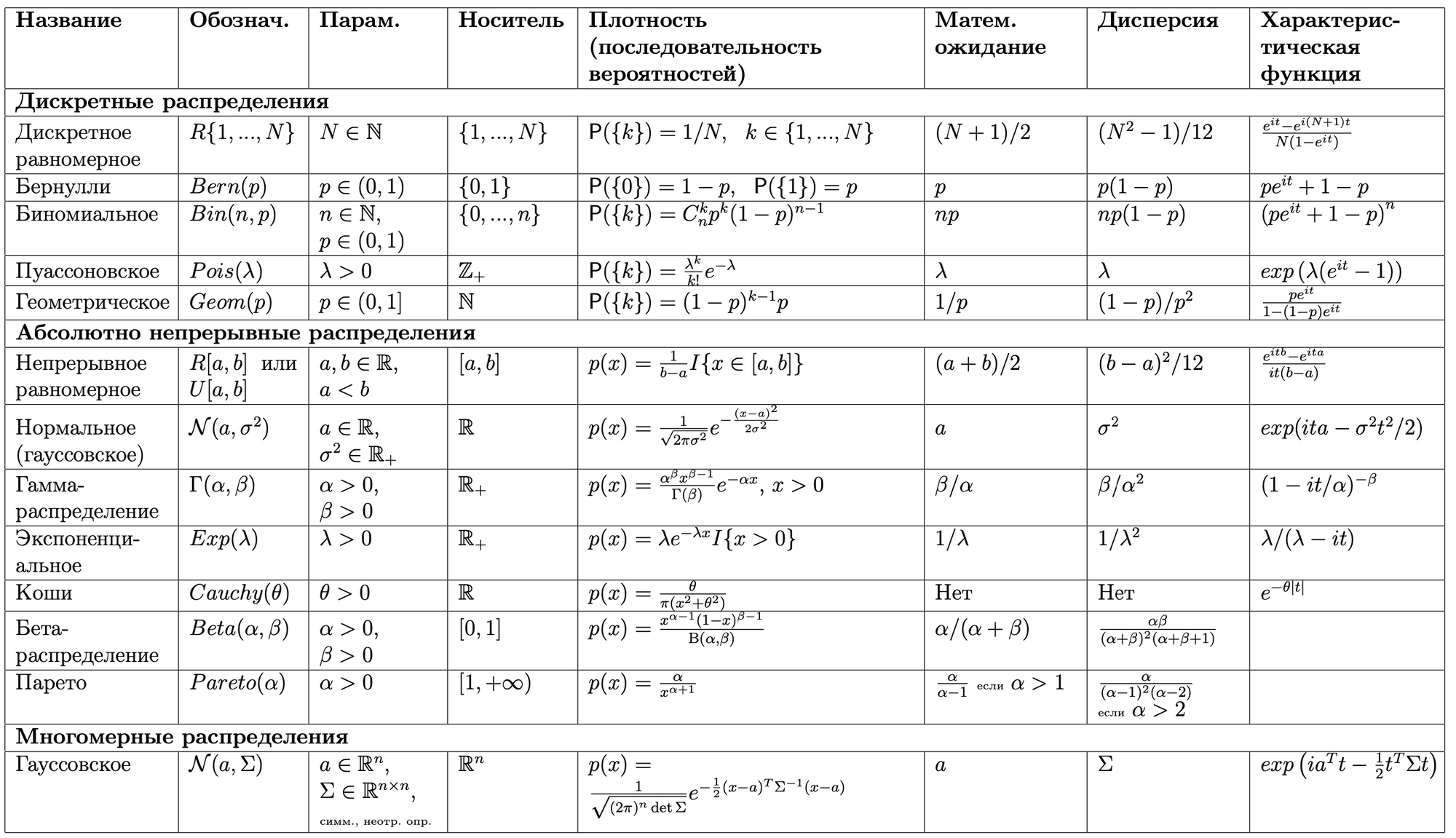
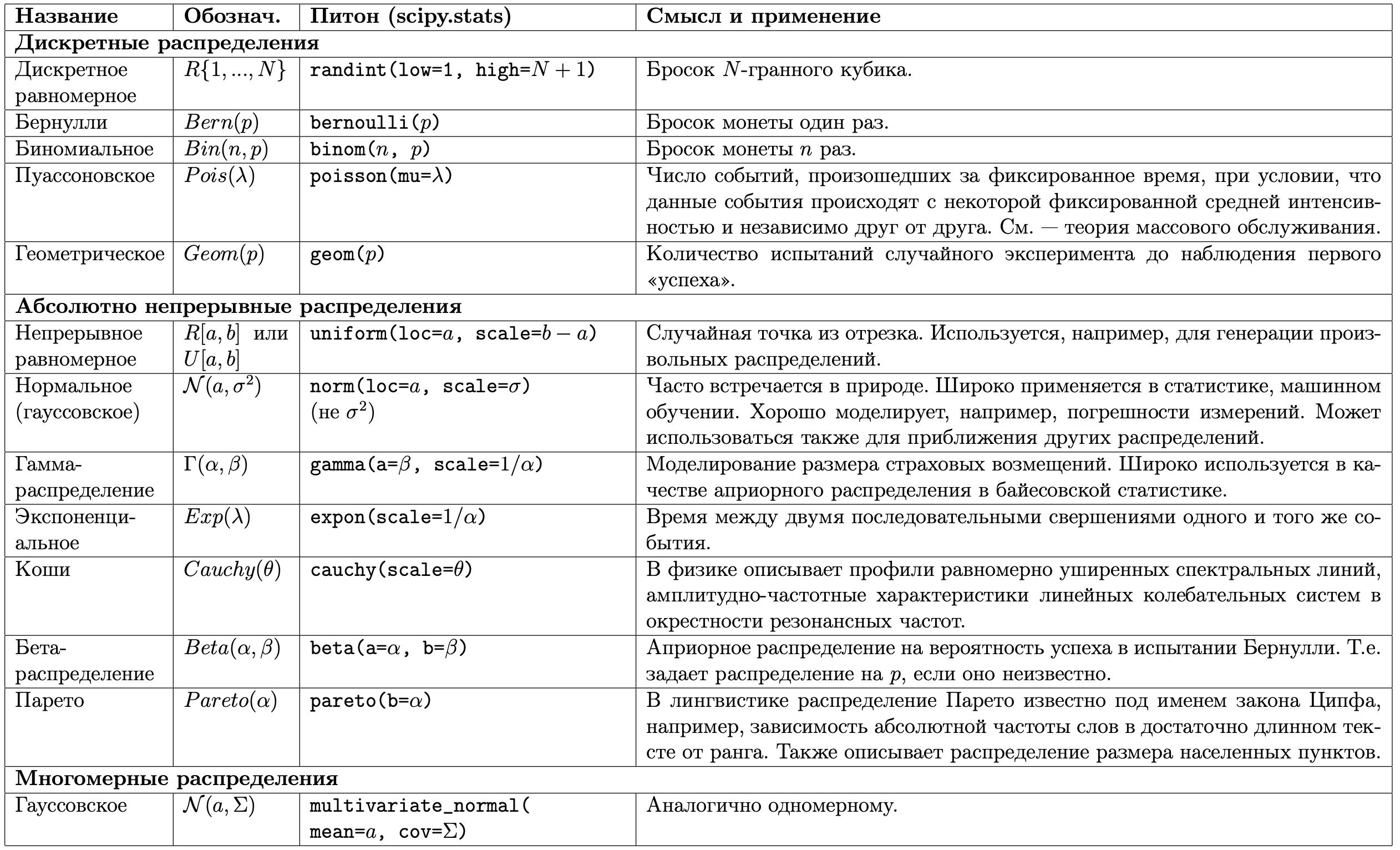
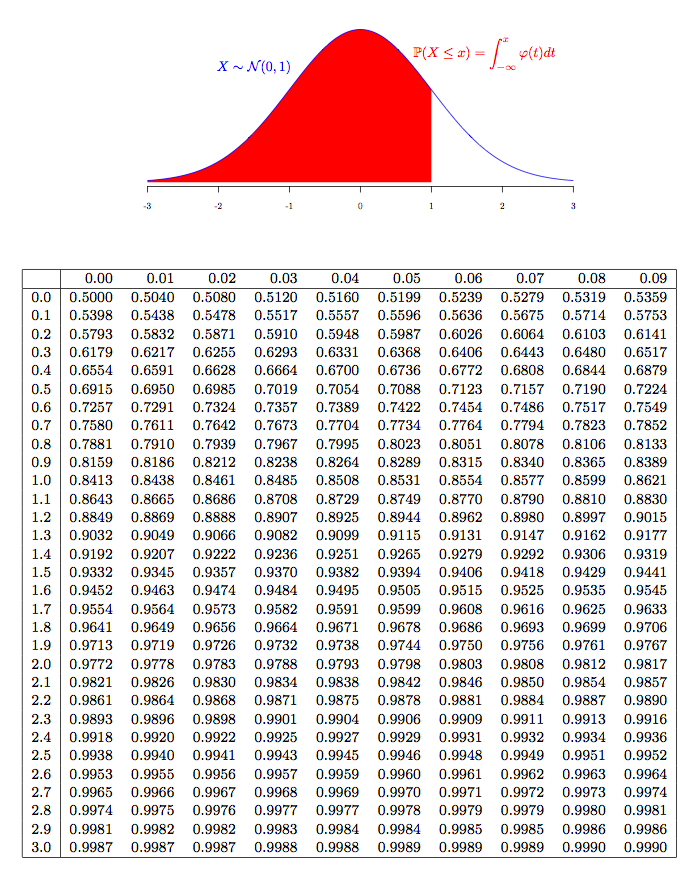
  7. Случайные величины. Функция распределения и ее свойства. Дискретные и абсолютно непрерывные распределения, плотность распределения. Важнейшие распределения: биномиальное, пуассоновское, геометрическое, равномерное, нормальное, Коши, экспоненциальное (показательное).
  8. Задание вероятностной меры на прямой с помощью функции распределения. Теорема о продолжении меры (б/д). 
  9. Распределение функций от случайных величин.
  10. Математическое ожидание случайной величины. Линейность математического ожидания. Математическое ожидание функции от случайной величины. Примеры комбинаторных задач, решаемых за счет линейности математического ожидания (теорема о числе треугольников в случайном графе).
  11. Независимость случайных величин. Свойства математического ожидания и дисперсии для независимых случайных величин. Ковариация и корреляция. Соотношение между независимостью и некоррелированностью.
  12. Моменты. Факториальные моменты. Дисперсия. Вычисление моментов для распределений из п. 7.
  13. Неравенства Маркова и Чебышёва. Применение в задаче о числе треугольников в случайном графе. Закон больших чисел для независимых (или даже попарно некоррелированных) одинаково распределенных величин с конечным вторым моментом (или даже по-разному распределенных, но с равномерно ограниченной дисперсией). Оценка уклонения для схемы Бернулли и ее соотношение с неравенством Чебышёва.
  14. Метод моментов (формула обращения). Пуассоновская аппроксимация (со слегка неаккуратным доказательством, но пониманием, где эта неаккуратность). Применения в задаче о числе треугольников в случайном графе (без детальных выкладок).
  15. Случайные векторы. Совместное распределение вероятностей. Многомерная функция распределения и ее свойства. Многомерная плотность распределения. Задание вероятностной меры в n-мерном пространстве (идея). 
  16. Распределение сумм независимых случайных величин. Формула свертки.
  17. Распределение функций от нескольких случайных величин. Математическое ожидание функции от нескольких случайных величин.
  18. Виды сходимости последовательностей случайных величин. Сходимость по вероятности слабее сходимости почти наверное (пример в одну сторону, в другую сторону – б/д). Интерпретация предельных теорем Пуассона и Муавра – Лапласа в терминах сходимостей.
  19. Усиленный закон больших чисел (в двух вариантах, оба б/д).
  20. Характеристические функции и их свойства. Разложение в ряд Тейлора. Вычисление характеристических функций для распределений из п. 7. Метод характеристических функций: теоремы единственности и непрерывности (б/д). Применение в задаче о сумме независимых пуассоновских величин.
  21. Центральная предельная теорема для сумм независимых одинаково распределенных случайных величин. Связь с предельной теоремой Муавра – Лапласа. Теорема Берри – Эссеена (б/д).
  22. Закон больших чисел без условия конечности второго момента. Соотношения между различными законами больших чисел (всего 4 формулировки).
  23. Понятие о случайном веб-графе.

Литература

  1. Севастьянов Б. А. Курс теории вероятностей и математической статистики
  2. Чистяков В.П. Курс теории вероятностей
  3. А.Н.Ширяев. ВЕРОЯТНОСТЬ .
  4. Introduction to probability for Data Science - Stanley H. Shan. [download]

Recommended extra material

  • Short lectures on measure theory: [playlist]
  • Short lectures on Probability Theory [playlist]
  • Probability theory course IMPA [playlist]
  • Probability theory course Harvard University [playlist]
  • Interactive videos on probability from 3Blue1Brown [video]
  • Lectures in introduction to probability (in russian) [playlist]