Probability Theory

Overview

Welcome to my course on Probability Theory for the second-year students of Bachelor’s Programs “Computer Science”, “Aerospace Engineering” and “Biomedical Engineering” at MIPT.

This is the first part of the course. We will devote this semester to the study of discrete probability theory, incluiding introductory notions of random variables and the way of computing their expected value, variance and correlation coefficient. In addition, the Markov and Tchebyshev inequalities will be introduced and we will prove the Tchebyshev's form of the weak law of large numbers.

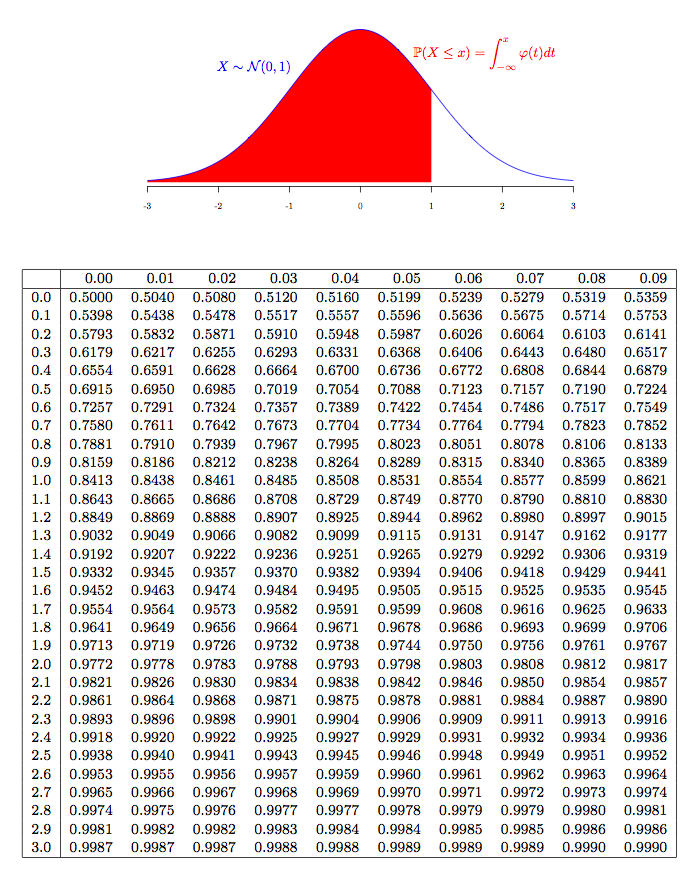
Next semester, we will generalize the concept of a random variable as a measurable function. We will extensively use the CDF and the PDF of random variables to compute all their interesting numerical characteristics. As a whole, we will completely construct the concept of a propability space. We will conclude our course with the proof of one of the main results in probability theory - the central limit theorem.

Problem sets

Problem set 1. Combinatorics

Problem set 2. Classical probability

Problem set 3. Geometric probability. Bernoulli scheme and independence.

Problem set 4. Conditional probability. Bayes Formula.

Problem set 5. Discrete random variables. Probability mass function.

Problem set 6. Expected value and Variance. Covariance.

Problem set 7. Discrete joint probability distributions.

Problem set 8. Simple random walk.

Problem set 9. De Moivre–Laplace theorem.

Attendance & Marks

Attendance list.

Marks.  

Topics discussed in lectures

Lecture 1 (04.02) Basics of combinatorics. Rule of sum and rule of product. Pigeon-hole principle. Permutations and combinations. Binomial and Multinomial theorem. Combinatorial identities (7 formulas).

Lecture 2 (11.02) Inclusion-exclusion principle. Random experiments and notion of probability. Probability in nature. Probability triple. Discrete sample space. Classical probability model.

Lecture 3 (18.02) Bernoulli scheme. k successes in n trials. Sum of all outcomes gives 1. Geometric probability. Probability of two people meeting.

Lecture 4 (25.02) Probability of getting success in first trial. Definition and examples of sigma-algebras. Algebra which is not a sigma-algebra. Measurable space. Probability measure-definition and properties.

Lecture 5 (04.03) Continuity of the probability measure. Probability of union of intersecting events and upper bound. Conditional probability. Theorem of multiplication. Independence of events (pairwise and mutually). Example of pairwise but not necessarily mutually independent events. Example on the neccesary conditions for mutually independence.

Lecture 6 (11.03) Partition of Omega. Total Probability Formula. Bayes Theorem. Monty-Hall problem. Problem on choosing an easy ticket. Notion of random variables. Number of successes in Bernoulli scheme as a random variable. Measurable function. Borel sigma-algebra. Probability Mass Function (PMF).

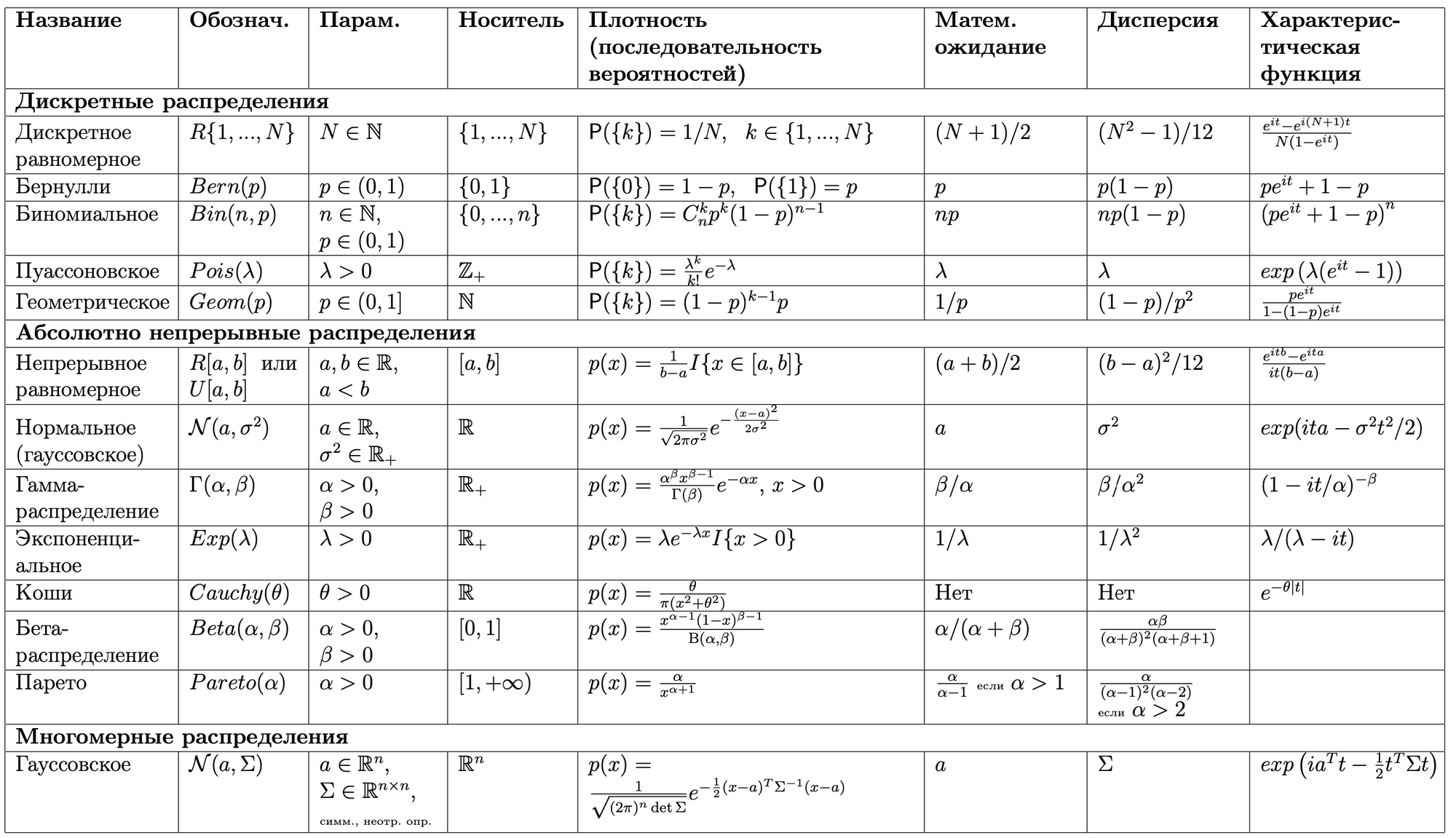
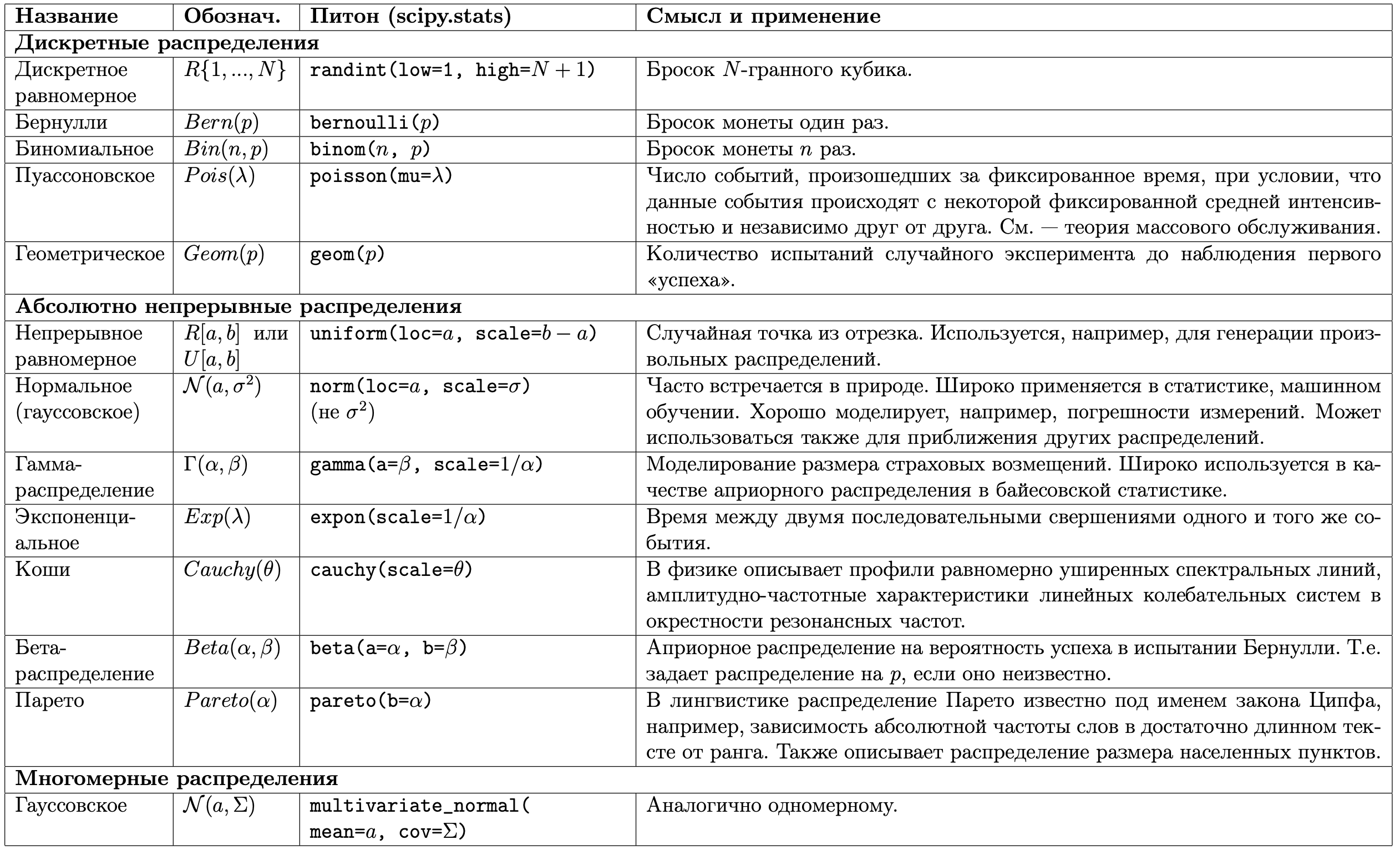
Lecture 7 (18.03) Independence of discrete random variables. Examples of discrete distributions (Bern(p), Bin(n,p), Geom(p), Pois(λ)). Expected value of a random variable. Problem on choosing an easy question at the exam.

Lecture 8 (25.03) Properties of the Expected value with proofs (5). Variance. Properties with proofs (3). Covariance. Example of dependent random variables with zero covariance.

Lecture 9 (08.04) Expected value and variance of random variables with distribution Ber(p), U({1,...,n}), Bin(n,p), Pois(λ). Properties of covariance (5). Variance of sum of n random variables. Correlation coefficient, definition and meaning. |corr(x,y)|<=1. Proof 1.

Lecture 10 (15.04) Notion of random graphs. Markov's inequality. Сhebyshev inequality. Cauchy–Bunyakovsky inequality. Application in the proof of the value of the correlation coefficient.

Lecture 11 (22.04) Weak Law of large numbers. General form of WLLN. Joint distribution of two random variables. Properties. Random walk.

Lecture 12 (29.04) Simple symmetric random walks. P(Sn=k). P(S1>0,...,Sn-1>0,Sn=k). P(Mn>=x)<=P(Sn>=x). Number of times a trajectory intersects zero.

Lecture 13 (06.05) De Moivre-Laplace Local limit Theorem. De Moivre-Laplace Local limit Theorem.

Exam Questions